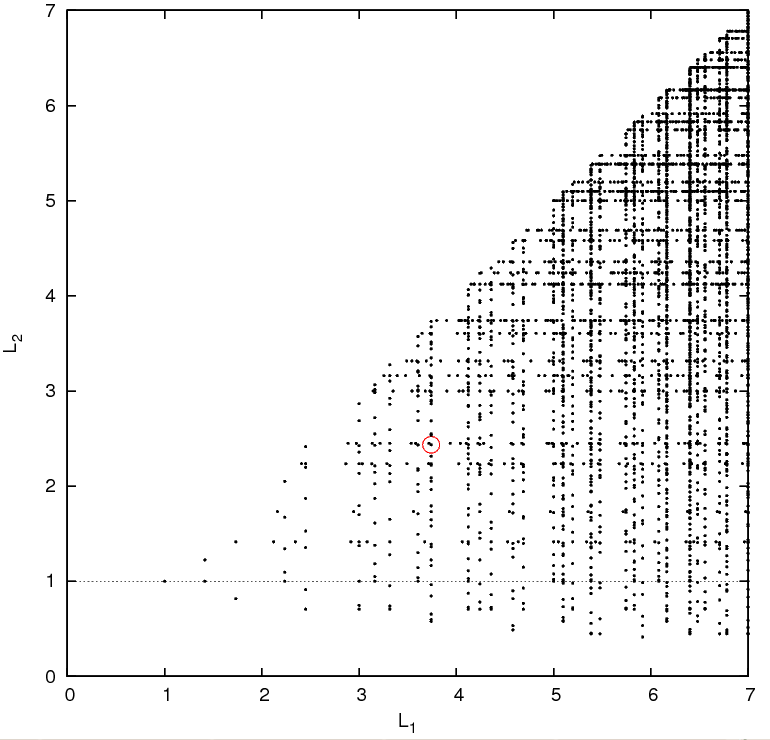
Possible side lengths L1 and L2 for the remapped cuboid, in units of the length Lbox of the original simulation cube. The third side length is given implicitly by the volume preserving condition L1 L2 L3 = 1.
This website provides companion material to the paper
"Embedding realistic surveys in simulations through volume remapping",
J. Carlson and M. White, ApJS 190(2010)311.
(preprint available at
arxiv:1003.3178),
One often wishes to make mock catalogs, generate simulated LyA forest spectra, or otherwise use a simulation to model a survey which has highly disparate dimensions. Running simulations in non-cubical geometries can be complicated, and one often does not generate the simulations for the particular geometry that they will later be used on.
By viewing the periodic cube as a hyper-torus one can devise "wrappings" of light rays which generate light-cones or cube remappings which allow non-cubical geometries, but this can become complex. We have a new way of thinking about generating non-cubical geometries from cubical simulations which is
The method works in 3D and maps a periodic cube of side length 1 into a cuboid (i.e. a non-cubical box) whose side lengths (L1, L2, L3) may chosen from a discrete but large space of possibilities. The following scatter plot shows some of the possible dimensions for the remapped cuboid.

Possible side lengths L1 and L2 for the remapped cuboid, in units of the length Lbox of the original simulation cube. The third side length is given implicitly by the volume preserving condition L1 L2 L3 = 1.
A useful subset of the possible remappings may be parameterized by a pair of integers, as outlined in this presentation given at a DES working group meeting.
Our software implementation of the cuboid remapping method may be downloaded as a gzipped tarball here. It consists of three main pieces of code:
The Python implementation is available in the python/ subdirectory of the tarball. It consists of the single file remap.py, and has no dependencies other than a Python interpreter. (Numpy will be used if available, but it is not required.) The Cuboid class is responsible for remapping points from the unit cube into a cuboid; it is initialized by passing the row vectors of a 3x3 invertible integer matrix. To use it in your own Python program, you would write, e.g.,
from remap import * C = Cuboid(u1=(2,1,0), u2=(0,0,1), u3=(1,0,0)) x,y,z = C.Transform(0.5, 0.5, 0.5)
Alternatively you can run remap.py as a program from the command line, to remap an entire text file of points into the cuboid geometry. E.g.
$ python remap.py u="2 1 0 0 0 1 1 0 0" in=input.dat out=stdout
The C++ implementation (found in the c++/ subdirectory) works the same way as the Python one, but since it is compiled it is much faster. To use it in your own program, you just need to include the header cuboid.h in your source code, then compile and link the source file cuboid.cpp into your program. E.g. in your source code you could write
#include "cuboid.h"
...
Cuboid C(2, 1, 0, 0, 0, 1, 1, 0, 0);
vec3d r = C.Transform(0.5, 0.5, 0.5);
Then you would compile your program with e.g.
$ g++ myprogram.cpp cuboid.cpp -o myprogram
The Python and C++ implementations must be initialized with the elements of a 3x3 invertible integer matrix, each of which uniquely specifies a cuboid remapping. A C++ program to generate such matrices may be found in the genremap/ subdirectory. For details see the README file in that directory.
In the demo/ subdirectory of our software package we include an interactive demo that shows how the unit cube is broken up into cells, which are then translated by integer offsets so that they form a cuboid. The following movie is a screen capture from that program.
Given the choice of a 3x3 invertible integer matrix, this Mathematica notebook shows the relevant calculations for determining the geometry of the remapped cuboid.
The following four panels show a single slice through a simulation, remapped in 2D into different configurations.
A thin slice through a simulation:



| Name | Size (kB) | Last modified |
| BoxRemap_DES09.pdf | 929 | 2010/01/02 |
| cuboidremap-1.0.tar.gz | 298 | 2010/03/15 |
| demo.avi | 5626 | 2010/03/15 |
| demoshot.png | 30 | 2010/03/15 |
| possremap.png | 41 | 2010/03/02 |
| remapmath.nb | 15 | 2010/03/15 |
| warp_0.png | 206 | 2010/01/02 |
| warp_1.png | 206 | 2010/01/02 |
| warp_2.png | 205 | 2010/01/02 |
| warp_3.png | 205 | 2010/01/02 |
Last modified Tue Mar 16 20:37:53 2010